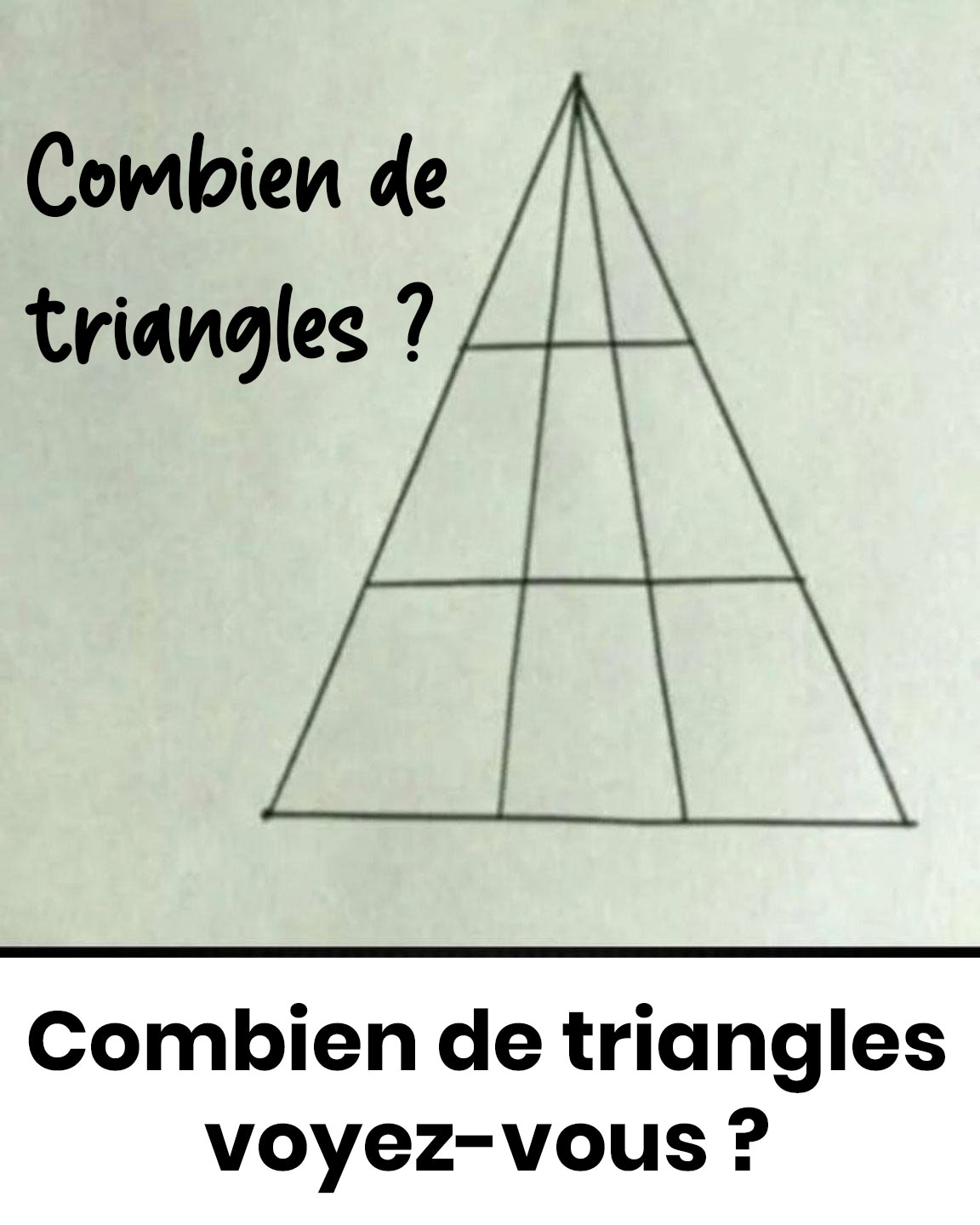
Combien de triangles voyez-vous sur cette image ? Le casse-tête qui piège (presque) tout le monde
Vous pensez avoir l’œil affûté ? Ce casse-tête visuel va peut-être vous faire douter !
À première vue, ce grand triangle divisé par plusieurs lignes parallèles semble anodin. On repère quelques triangles ici et là… puis on additionne. Facile, non ? Et pourtant, la majorité des gens se trompent !
Ce défi, aussi simple qu’il en a l’air, cache une vraie leçon de logique et de perception. Prêt(e) à voir ce que beaucoup ne voient pas ?
Le piège des triangles cachés
Notre cerveau adore simplifier. Il repère d’abord les petits triangles évidents, ceux qui sautent aux yeux, et oublie souvent les grands formés par la combinaison de plusieurs zones. Résultat : on sous-estime presque toujours le total.
Dans la version classique du puzzle (un grand triangle divisé en 4 rangées par trois lignes parallèles à la base), la bonne réponse n’est ni 16 ni 24… mais 27 triangles exactement !
La plupart des erreurs viennent d’un triangle composite oublié : un grand triangle qui s’étend sur trois niveaux, ou un “demi-large” sur le côté.
Comment compter sans se tromper ?
Pour éviter les oublis, suivez une méthode claire, étape par étape :
1. Comptez les triangles orientés vers le haut :
-
Hauteur d’un niveau : 10
-
Hauteur de deux niveaux : 6
-
Hauteur de trois niveaux : 3
-
Hauteur de quatre niveaux : 1
➡️ Sous-total : 10 + 6 + 3 + 1 = 20
2. Ajoutez les triangles inversés (vers le bas) formés par l’imbrication des lignes :
➡️ 7 triangles “vers le bas”
Total final : 20 + 7 = 27 triangles.
Astuce mnémotechnique : souvenez-vous de la formule magique “20 en haut + 7 en bas”.
La formule secrète pour ne plus jamais vous tromper
Si vous aimez les mathématiques élégantes, voici une formule qui calcule automatiquement le nombre total de triangles pour ce type de figure :
T(n)=n×(n+2)×(2n+1)8T(n) = \frac{n × (n + 2) × (2n + 1)}{8}
où n est le nombre de rangées.
Appliquons-la au cas classique (n = 4) :
T = 4 × 6 × 9 ÷ 8 = 27.
Simple, rapide et exact !
Les erreurs les plus fréquentes
-
Oublier les grands triangles trans-niveaux. Ils sont discrets mais essentiels.
-
Négliger les triangles inversés. Moins visibles, ils sont pourtant bien là.
-
Inventer des lignes verticales. Certaines variantes du puzzle en ont, d’autres non : attention à la configuration exacte.
-
Compter deux fois les mêmes formes. Allez toujours du plus petit au plus grand, sans sauter d’étape.
Envie d’aller plus loin ?
-
Testez la formule avec d’autres valeurs : essayez n = 3 ou n = 5, et voyez si vous trouvez le bon total.
-
Faites-en un défi chronométré : donnez-vous 60 secondes pour atteindre 27.
-
Partagez le puzzle à vos amis : celui qui trouve du premier coup mérite son titre de maître des casse-têtes !
Conclusion
Derrière une simple figure géométrique se cache un vrai défi de logique et d’observation. Ce puzzle nous rappelle que l’œil peut être trompeur, mais qu’un esprit méthodique trouve toujours la vérité.
La prochaine fois qu’on vous demandera “Combien de triangles vois-tu ?”, vous saurez répondre sans hésiter — et expliquer pourquoi.