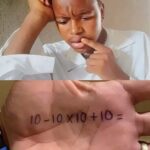Pouvez-vous trouver la solution à cette équation ?

admin1 février 2025

Les écoliers adorent les petits défis mathématiques, surtout lorsqu’ils paraissent simples au premier abord. Pourtant, lorsqu’il s’agit pour les parents de les vérifier, l’histoire peut vite se compliquer. Une équation comme 6 ÷ 2(1 + 2) = ? en est le parfait exemple : elle semble élémentaire, mais elle suscite régulièrement des débats animés sur Internet.

Pourquoi cette confusion ? Examinons cela en détail.

Un problème de notation et de règles mathématiques

Lorsqu’on rencontre une équation de ce type, l’erreur la plus courante est de mal appliquer les règles de priorité des opérations. Ces règles sont souvent enseignées à l’aide de l’acronyme PEMDAS (Parenthèses, Exposants, Multiplication et Division, Addition et Soustraction). Un principe essentiel à retenir est que la multiplication et la division ont le même niveau de priorité et doivent être résolues de gauche à droite.

Voyons comment appliquer cette règle à notre équation :

Résoudre d’abord les parenthèses
L’équation devient alors :
Appliquer les opérations dans l’ordre de lecture
Contrairement à certaines idées reçues, le terme 2(3) ne doit pas être traité comme une priorité absolue, mais comme une simple multiplication.

D’abord, la division :

Ensuite, la multiplication :

Résultat final : 9

D’où vient le doute ?

Beaucoup de gens interprètent le terme 2(3) comme une multiplication implicite qui aurait la priorité sur la division. Cette confusion vient en partie de la notation mathématique : en algèbre, la notation a(b) est souvent utilisée pour indiquer une multiplication factorisée, ce qui peut induire en erreur.

Cependant, en arithmétique standard, la multiplication implicite ne prime pas sur la division. Il faut donc bien lire et résoudre les opérations de gauche à droite lorsqu’elles ont la même priorité.

Une leçon d’importance pour l’apprentissage des maths

Ce type d’exercice rappelle à quel point il est crucial d’appliquer les règles mathématiques avec rigueur. Les enseignants doivent insister sur ces conventions pour éviter les erreurs d’interprétation, et les parents peuvent aussi revoir ces principes avec leurs enfants pour s’assurer qu’ils sont bien assimilés.

Conclusion

Les mathématiques ne sont pas seulement une question de calculs, mais aussi de convention et de rigueur. Une simple équation comme 6 ÷ 2(1 + 2) peut prêter à confusion si l’on n’applique pas correctement les règles de priorité.

Alors, la prochaine fois que vous ferez face à ce genre de dilemme mathématique, souvenez-vous de PEMDAS et lisez attentivement l’équation avant de trancher. Et surtout, amusez-vous avec les maths, car elles sont pleines de surprises !